cdfTnc#

Purpose#

The integral under the noncentral Student’s \(t\) distribution, from \(-∞\) to x.

Format#

p = cdfTnc(x, df, nonc)#

Parameters:

x (NxK matrix) – values of upper limits of integrals.
df (LxM matrix) – ExE conformable with x, the degrees of freedom, \(df > 0\).
nonc (PxQ matrix) – ExE conformable with x, the noncentrality parameter. This is the square root of the noncentrality parameter that sometimes goes under the symbol \(\lambda\).

Returns:

p (max(N,L,P) by max(K,M,Q) matrix) – Each element in p is the cumulative distribution function of the noncentral Student’s t distribution evaluated at the corresponding element in x.

Examples#

Noncentral t distributions with different parameters.#

// Values to find cdf at
x = seqa(0, 0.2, 101);

// Noncentrality parameter
nonc = 5;

// Degrees of freedom
df = 1~2~5~10~100;

// Call cdfTnc
p = cdfTnc(x, df, nonc);
plotxy(x, p);

After running above code,

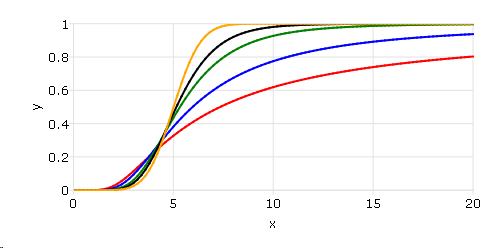
Noncentral t distributions with different degree of freedoms.#

// Values to find cdf at
x = seqa(-5, 0.5, 41);

// Noncentrality parameter
nonc = seqa(0, 0.5, 7);

// Degrees of freedom
df = 10;

p = cdfTnc(x, df, nonc');
plotxy(x, p);

After running above code,

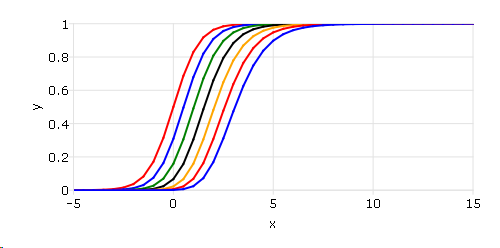
Remarks#

cdfTc(x, df) = 1 - cdfTnc(x, df, 0)