cdfEmpirical#
Purpose#
Computes the cumulative distribution function (cdf) of an empirical distribution.
Format#
- { f, break_points } = cdfEmpirical(x[, bins])#
- Parameters:
x (Nx1 vector) – Data vector.
bins (scalar or vector) – Optional input. If scalar, an evenly spaced vector with bins elements is created between x_min and x_max. If vector, GAUSS uses the passed vector as the values at which to find empirical cdf.
- Returns:
f (matrix), (N+1) x1 vector) – cdf values, where N is equal to bins if bins is a scalar or number of rows in bins if bins is a vector.
breakpoint (Nx1 vector) – break points used to calculate cdf values.
Examples#
new;
cls;
rndseed 2223;
// Create a random vector
x = rndn(30, 1);
// Sort x for the first column
x = sortc(x, 1);
// Get empirical cdf of x
f = cdfEmpirical(x);
// Add negative infinity (__INFN) for probability equal to 0.
print (__INFN|x)~f;
// Plot empirical distribution
plotCDFEmpirical(x);
// Get normal cdf of x
fnormal = cdfN(x);
// Plot theoretical distribution
plotAddXY(x, fnormal);
After above code,
-INF 0.00000000
-2.3124206 0.033333333
-1.6240227 0.066666667
-1.2763153 0.10000000
-0.82532512 0.13333333
-0.81574278 0.16666667
-0.64338729 0.20000000
-0.59625173 0.23333333
-0.49725006 0.26666667
-0.47855430 0.30000000
-0.39340284 0.33333333
-0.36201638 0.36666667
-0.063830011 0.40000000
-0.0064523646 0.43333333
0.23570074 0.46666667
0.32355136 0.50000000
0.37501508 0.53333333
0.39847826 0.56666667
0.50039685 0.60000000
0.68900341 0.63333333
0.69132515 0.66666667
0.72246796 0.70000000
0.76893134 0.73333333
1.0221019 0.76666667
1.0638924 0.80000000
1.1274880 0.83333333
1.2610791 0.86666667
1.4445086 0.90000000
2.0295113 0.93333333
2.1240430 0.96666667
3.1784008 1.0000000
The plot is
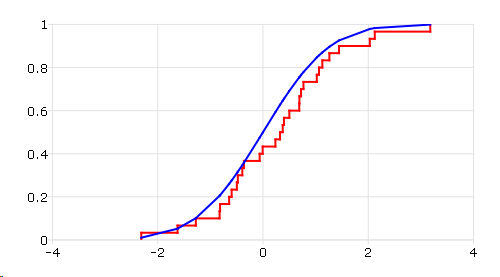
Remarks#
f is the integral from \(-\infty \text{ to } x\) of the empirical distribution function.
See also
Functions plotCDFEmpirical()
